Rotenix Bridging AI and Optimization: How LLMs Can Solve Complex Decision Problems

The Computational Challenge of Complex Optimization

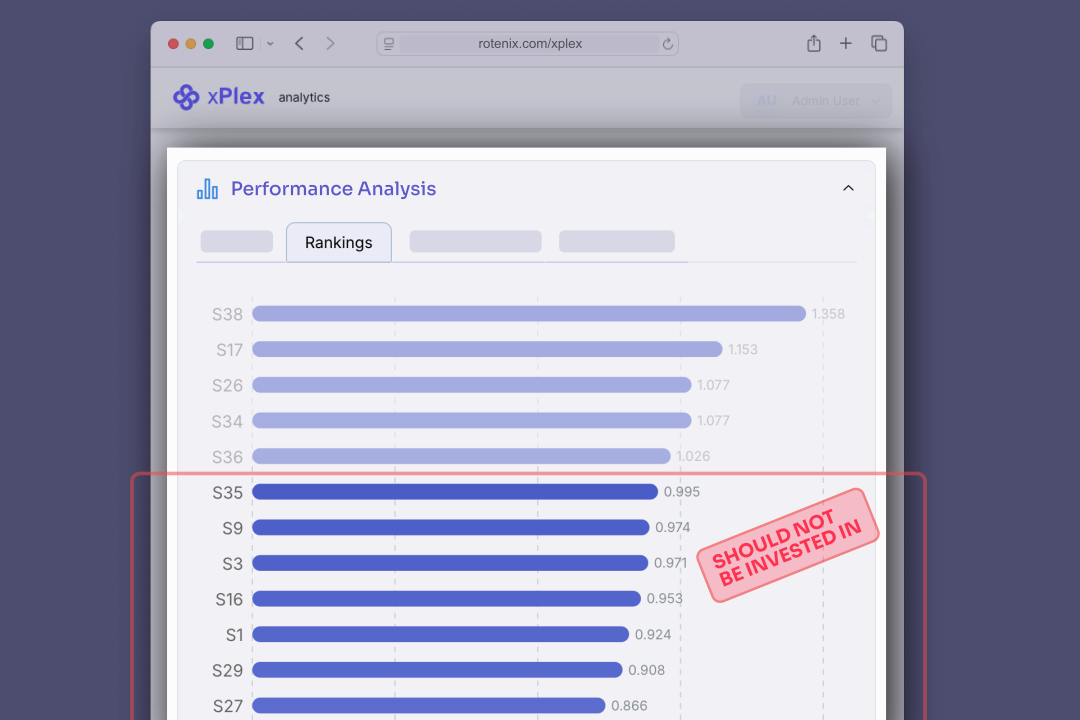
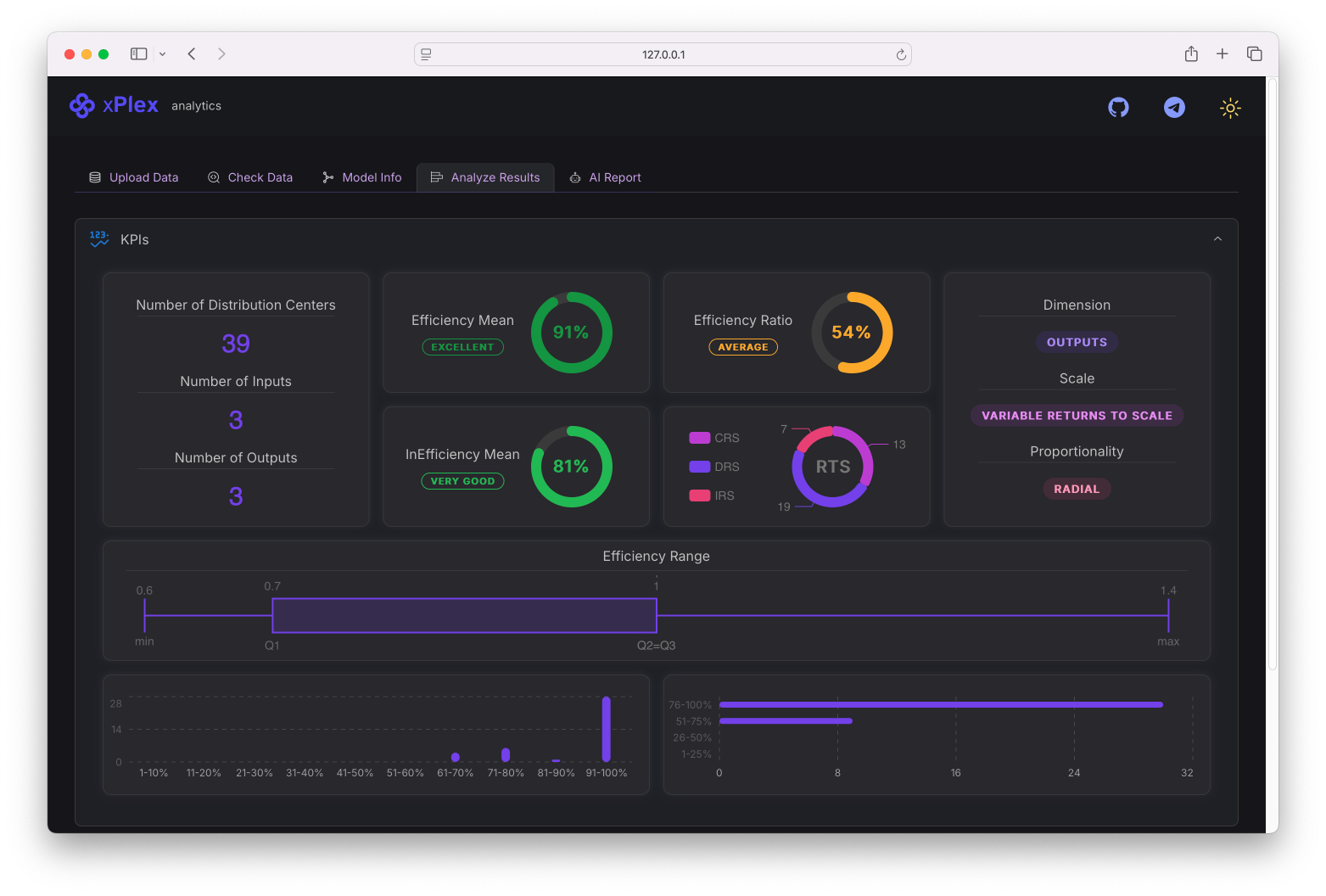
Complex optimization problems like supply chain management present a fundamental challenge for Large Language Models (LLMs). These problems often involve thousands or even millions of decision variables, constraints, and parameters that must be considered simultaneously to find optimal solutions.

To understand the scale of this challenge, consider a global supply chain optimization problem. A realistic model might include:

• Hundreds of production facilities with different capacities and costs
• Thousands of products with various specifications
• Multiple transportation modes with different costs and transit times
• Numerous demand points with fluctuating requirements
• Seasonal variations, lead times, and inventory constraints

Representing this complexity requires an enormous amount of data. If we were to express all these variables, constraints, and their relationships as tokens for an LLM to process, we would quickly exceed the token limitations of even the most advanced models. Even models with 100,000+ token context windows would struggle to hold the complete mathematical representation of complex real-world optimization problems.

Furthermore, even if an LLM could theoretically ingest all this information, it lacks the specialized algorithms necessary to efficiently search through the vast solution space. Optimization problems often require techniques like linear programming, mixed-integer programming, or constraint programming—mathematical approaches that LLMs simply aren’t designed to execute internally.

Even models with 100,000+ token context windows would struggle to hold the complete mathematical representation of complex real-world optimization problems.

The Model Context Protocol (MCP): A Bridge Between Worlds

The Model Context Protocol (MCP) offers an elegant solution to this fundamental limitation. MCP establishes a standardized communication framework that allows LLMs to interact with specialized optimization solvers like Gurobi, CPLEX, or OR-Tools.

Rather than attempting to solve complex optimization problems internally, the LLM’s role becomes:

1. Understanding the problem from natural language descriptions
2. Formulating the mathematical model with variables, constraints, and objectives
3. Translating this into a format the specialized solver can understand
4. Interpreting the results and communicating them back to humans

The key innovation of MCP is the recursive feedback loop it establishes. The LLM sends the formulated problem to the solver, which then returns solutions or diagnostics. This information is fed back to the LLM, which can then refine the problem formulation, request clarification from users, or explain the solution in natural language.

This approach leverages the complementary strengths of both systems: the LLM’s understanding of natural language and context, combined with the solver’s computational efficiency and mathematical rigor.

The key innovation of MCP is the recursive feedback loop it establishes. The LLM sends the formulated problem to the solver, which then returns solutions or diagnostics. This information is fed back to the LLM, which can then refine the problem formulation, request clarification from users, or explain the solution in natural language.

Architectural Approaches for LLM-Solver Integration

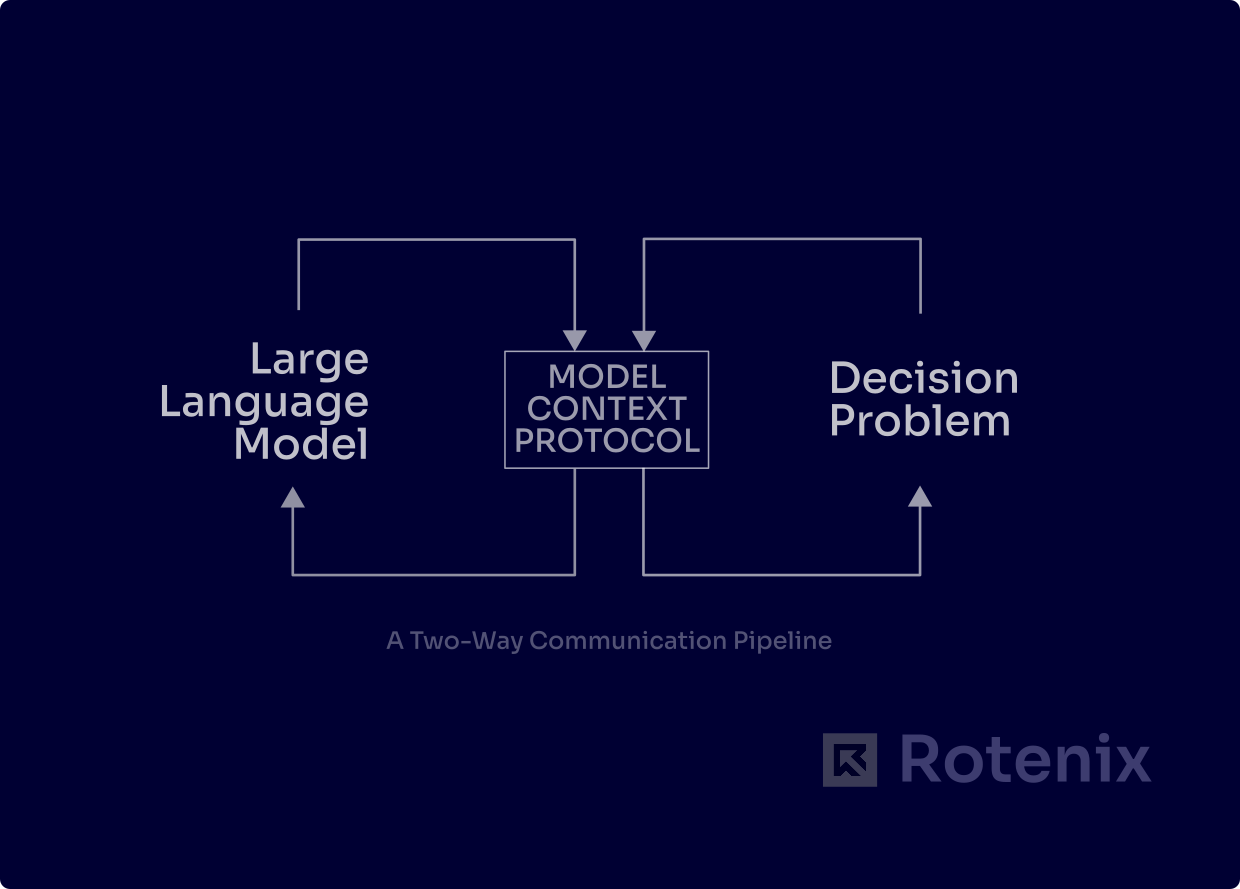
Two-Way Communication Pipeline

The simplest architecture establishes a bidirectional pipeline between the LLM and solver. The LLM functions as a natural language interface, translating user requirements into mathematical models that the solver can process. After the solver finds a solution, the LLM interprets these results and presents them in an understandable format.

What makes this architecture powerful is the inclusion of feedback mechanisms. When the solver encounters issues—perhaps an infeasible constraint or unbounded objective—it communicates this back to the LLM, which can then suggest modifications or ask the user for clarification.

For example, if a supply chain model proves infeasible, the solver might identify which constraints are causing the issue. The LLM can then explain these technical details to the user in plain language: “Your requirement to deliver all products within 24 hours while using only ground transportation isn’t possible given the distances involved. Would you like to extend the delivery window or allow air freight for certain routes?”

Multi-Agent Collaborative Framework

A more sophisticated approach involves creating specialized agents that work together to solve different aspects of the optimization problem. This might include:

• A problem formulation agent that translates natural language into mathematical models
• A constraint validation agent that ensures the model accurately reflects real-world limitations
• A solution interpretation agent that explains results in context-appropriate language
• A coordinator agent that manages the workflow between components

This architecture provides greater modularity and extensibility. New solver types can be integrated without redesigning the entire system, and domain-specific knowledge can be incorporated into appropriate agents. For instance, a supply chain specialist agent might understand industry-specific constraints, while a financial specialist agent could focus on cost implications.

Interactive Refinement Architecture

The interactive refinement approach acknowledges that complex optimization problems often can’t be perfectly formulated on the first attempt. Instead, this architecture starts with a simplified version of the problem and progressively refines it through multiple iterations.

The process begins with the LLM creating a basic model based on the user’s initial description. The solver attempts to find a solution, and the results—along with any issues encountered—are fed back to the LLM. Based on this feedback and additional user input, the LLM refines the model, perhaps adding constraints, adjusting parameters, or restructuring objectives.

This approach is particularly valuable for complex real-world problems where users themselves may not fully understand all constraints until they see preliminary results. The interactive nature allows for exploration of the solution space and progressive discovery of the true problem structure.

Domain-Specific Template System

The template-based architecture focuses on reliability and efficiency by providing pre-built frameworks for common optimization problem types. Instead of formulating problems from scratch, the LLM selects and customizes appropriate templates based on the user’s requirements.

For example, a vehicle routing template might already include standard constraints for vehicle capacity, time windows, and driver shifts. The LLM’s task is to identify the specific parameters needed for the user’s scenario and populate the template accordingly.

This approach significantly reduces formulation errors and improves efficiency, especially for well-understood problem classes. It also makes the system more accessible to users with limited optimization knowledge, as the templates incorporate best practices and standard formulations.

Conclusion

The integration of LLMs with optimization solvers through protocols like MCP represents a significant advancement in decision support systems. By combining the natural language understanding and contextual awareness of LLMs with the computational power of specialized solvers, we can address complex optimization problems that neither system could handle alone.

As these integrated systems evolve, we can expect to see increasingly sophisticated applications in supply chain management, resource allocation, scheduling, and other domains where computational complexity has traditionally been a barrier to AI adoption.

The future of AI-powered decision-making lies not in forcing LLMs to become optimization engines, but in creating symbiotic systems where each component contributes its unique strengths to solve problems that matter in the real world.